Traditional origami has a set of rules which flods are allowable and which are forbidden. Generally, evey fold should arise form the previous folds or edges of the sheet of paper. There should be no folds "to somebody's eye".
Humiaki Huzita in 1992 has formulated set of origami axioms:
1.Given two distinct points p1 and p2, there is a unique fold that passes through both of them.
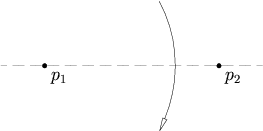
2.Given two distinct points p1 and p2, there is a unique fold that places p1 onto p2.
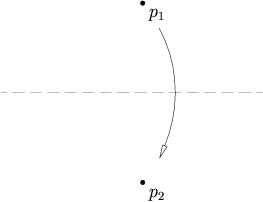
3.Given two lines l1 and l2, there is a fold that places l1 onto l2.
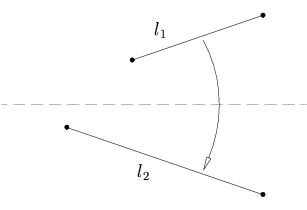
4.Given a point p1 and a line l1, there is a unique fold perpendicular to l1 that passes through point p1.
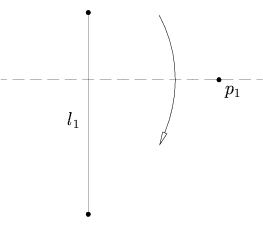
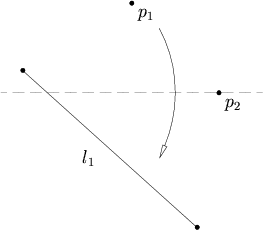
5.Given two points p1 and p2 and a line l1, there is a fold that places p1 onto l1 and passes through p2.
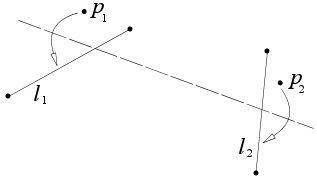
6.Given two points p1 and p2 and two lines l1 and l2, there is a fold that places p1 onto l1 and p2 onto l2.
A seventh axiom overlooked by Huzita was discovered by Koshiro Hatori in 2002:
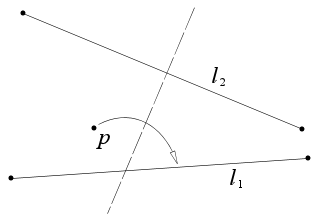
7.Given one point p and two lines l1 and l2, there is a fold that places p onto l1 and is perpendicular to l2.
These axioms, joined, can form more powerful geometric tools, such as angle bisector or perpendicular bisector